軌道要素の可視化：動く説明図を作りました

プラネタリウム事業部のとよだです。

今回は、小惑星や彗星の軌道を示す際によく登場する「軌道要素」について、簡単に解説してみるべく、「パラメータを変化させると動く説明図」を作ってみました。

軌道要素について
動かせると面白い
図を描くことについて
ステラナビゲータとの比較
まとめ
おまけ

軌道要素について

みなさんは、「軌道要素」をご存知でしょうか。

たぶん一般的には、マニアックすぎて興味もないのではと思いますが、天文をやっている人だと釈迦に説法である可能性もある…。ということでこの記事は、恐ろしく狭いターゲットにしか響かないのではという気がしなくもないのですが、気付かないことにしたいと思います。食わず嫌いせず、ちょっとぐりぐりしてみると、案外楽しいはず…。

さて軌道要素とは、天体の軌道を表すパラメータの組み合わせです。太陽系内では、支配的な重力源が太陽そのものに一極集中しているので、その周りの軌道を比較的シンプルなパラメータで表すことができます。彗星や小惑星ではおなじみで、ステラナビゲータでもよく（？）見かけます。

各パラメータの意味合いは、言葉からもなんとなく想像はでき（るものもあり）ますが、まとめるとWikipediaにあるような図になります。

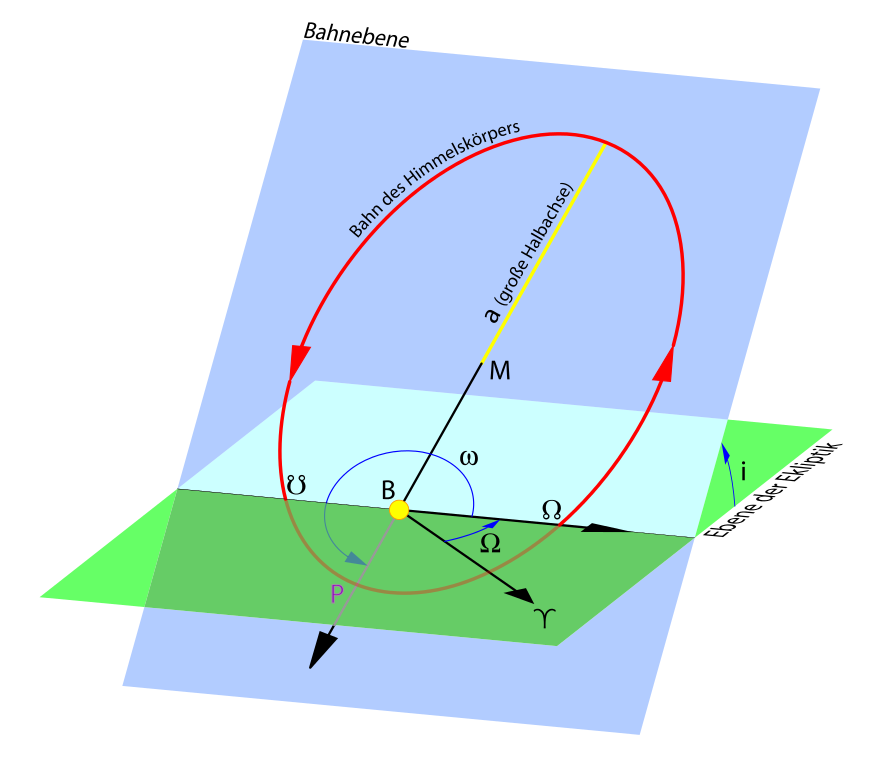
これが…わたしには分かりにくい。どこの角度のことを言っているのか…と思う場面が割とあります。軸と角度がもっと分かりやすければいいのに。

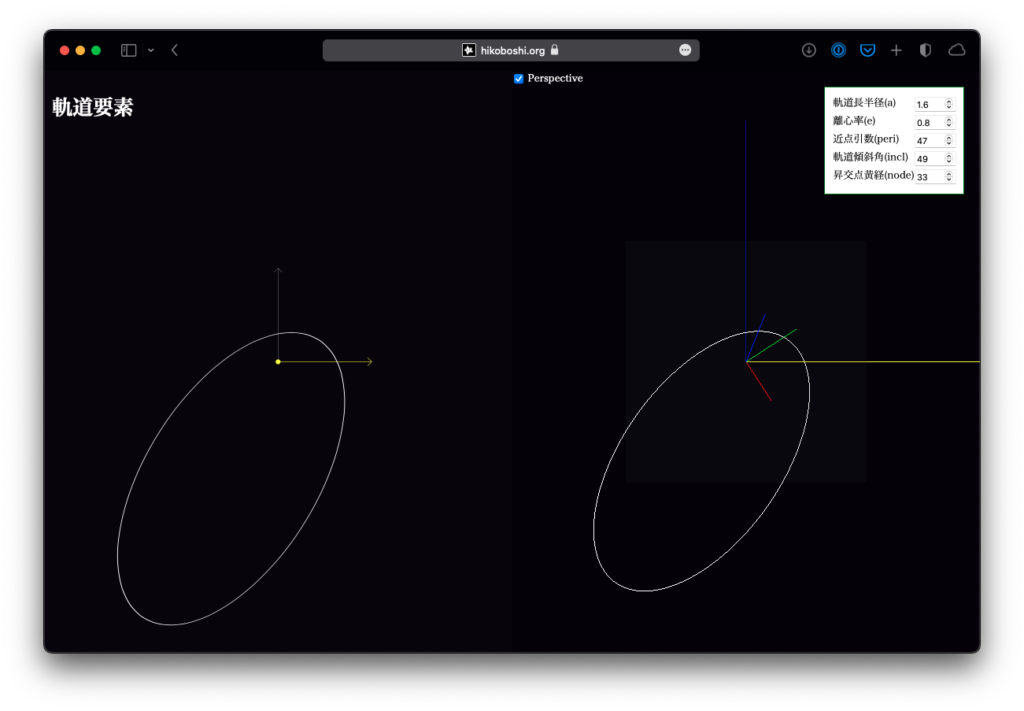
ということで、「動く説明図」を作ってみました。

軌道要素説明図

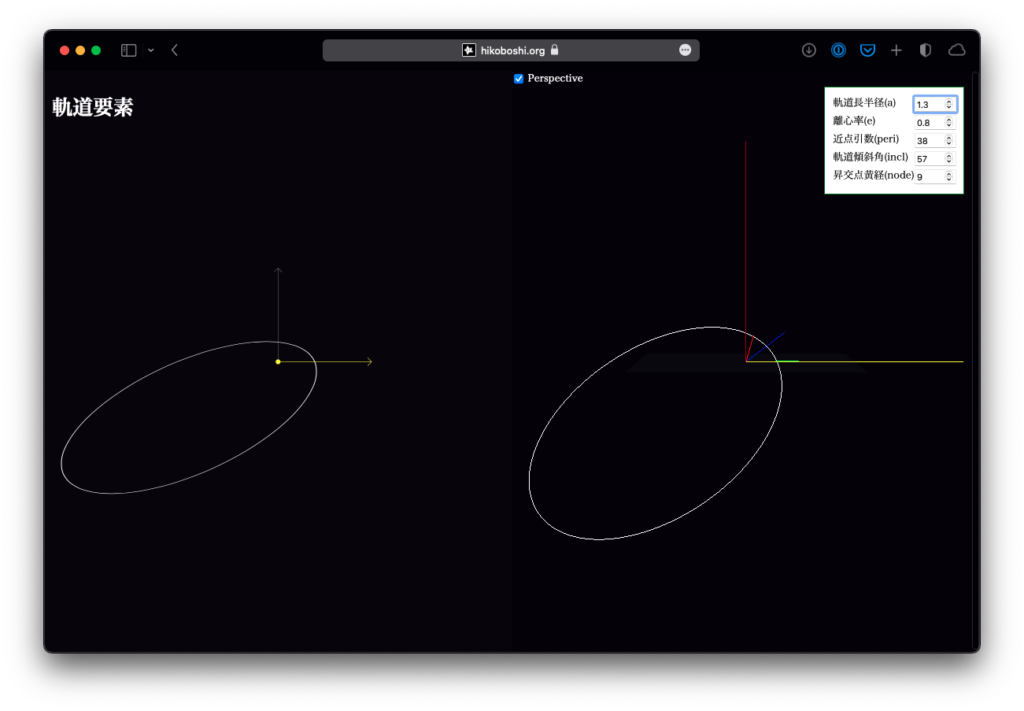
開くと左右に同じ図が出ていますが、左側はSVGで描いた平面図、右側はWebGLで書いた立体図です。右側についてはマウスでぐりぐり視線が変えられますので、立体感を確認したい時は右側を動かしてみてください。

後半に書きますが、この図は（平面版のほうを）SVGで直接描いている都合で、離心率が0 <= e < 1の範囲のものしか描けません。あらかじめご了承ください。

動かせると面白い

いくつか動かしてみましょう。

まず大前提として、計算そのものは抽象的なので特に決まりはないですが、イメージとしては日心黄道直交座標＝「太陽を原点として、黄道面（地球の平均軌道面）をXY平面、X軸を春分点方向にとった座標」を思い浮かべ、太陽の北側から軌道を眺めている状態を想像します。

要するに「太陽中心で地球の軌道面を上から見ている」ということです。

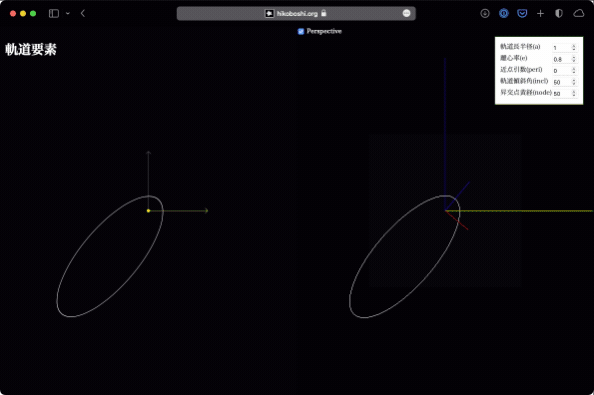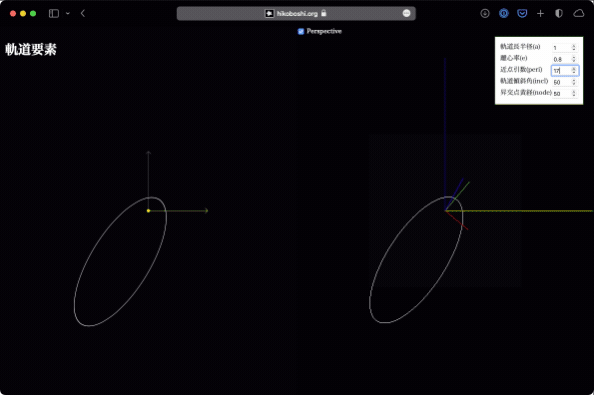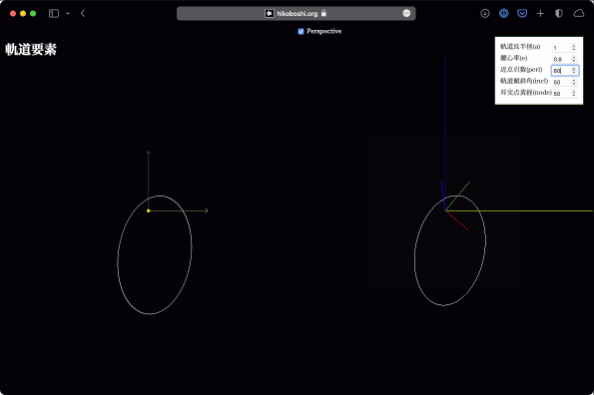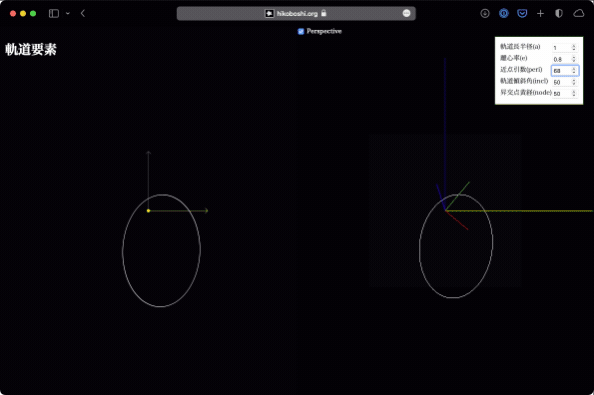
軌道長半径、離心率

これはいじらなくてもなんとなく想像ができますが、実際にやってみれば一目瞭然。軌道が大きくなったり、円から楕円に変わったりします。

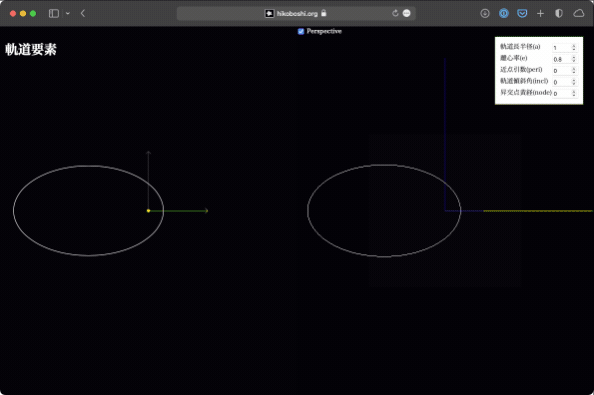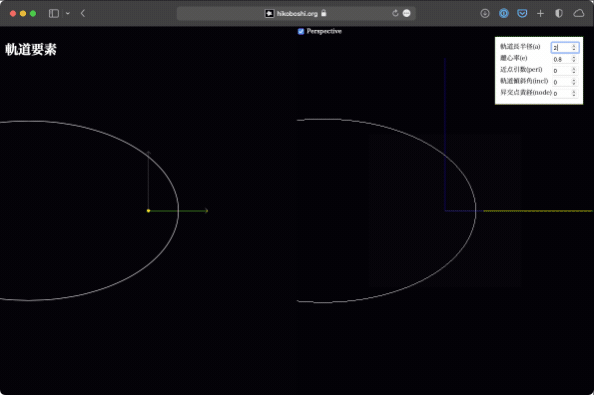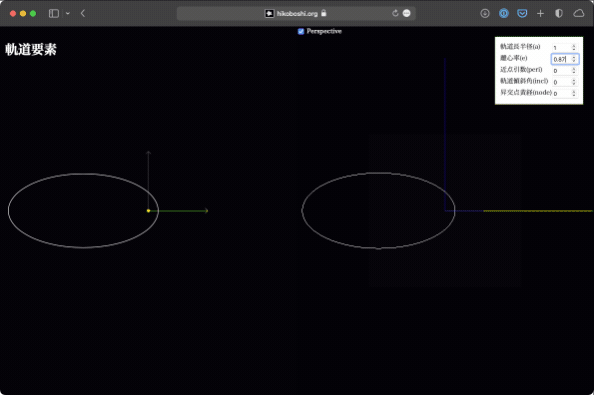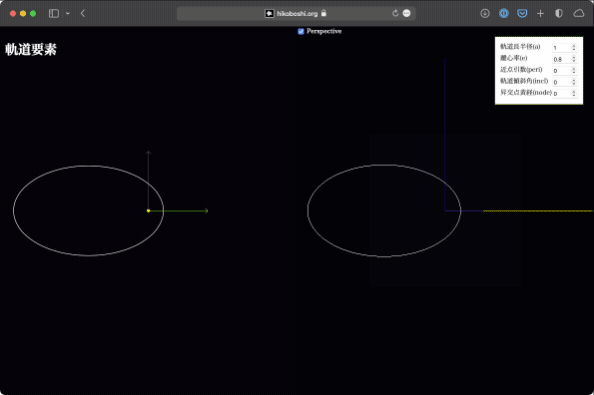
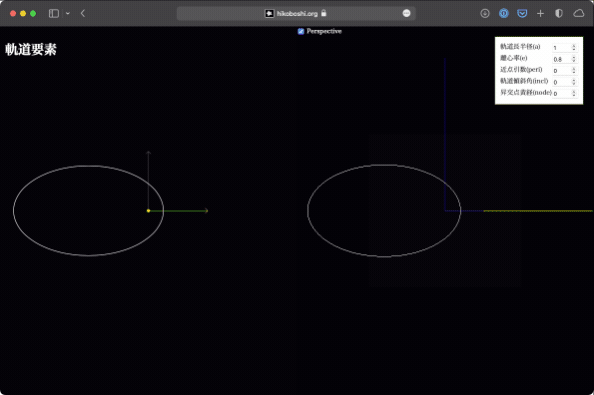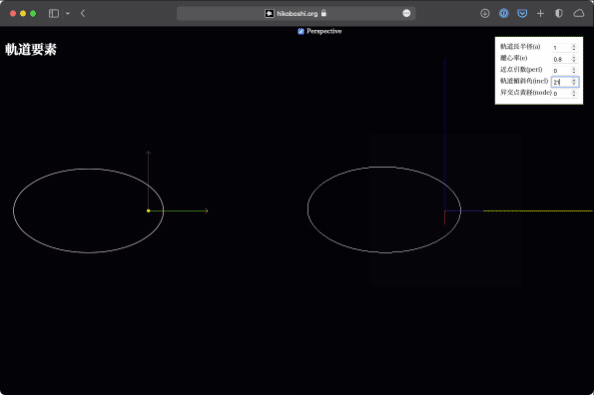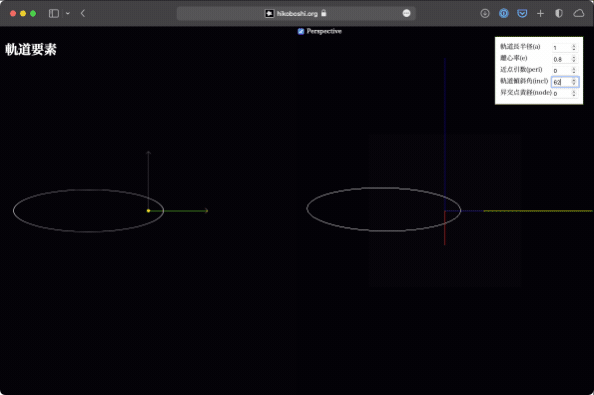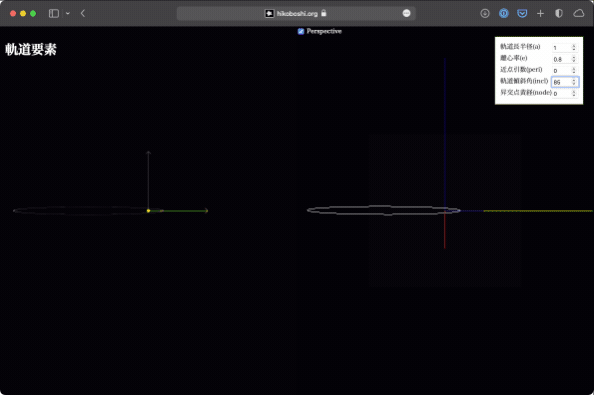
軌道傾斜角

これは黄道面と軌道面の成す角です。この値により、軌道が黄道面から立体的に立ち上がることになります。値を変化させると、なるほど真上から見ると軌道が潰れるように見えるわけですね。

平面で見ていると引き続きわかりにくいので、立体版をぐりぐりして確認してみてください。ひとたびイメージができてしまえば、ただ潰れているだけなのに立体的に見えるようになります…（暗示）。

Wikipediaを見ると、「逆行軌道は90-180度となるように指定」などと書かれていますが、何のことはありません。軌道傾斜角が90度を超えると、真上から見た時には逆回りになるので、値を統一的に扱えるというだけのことです。

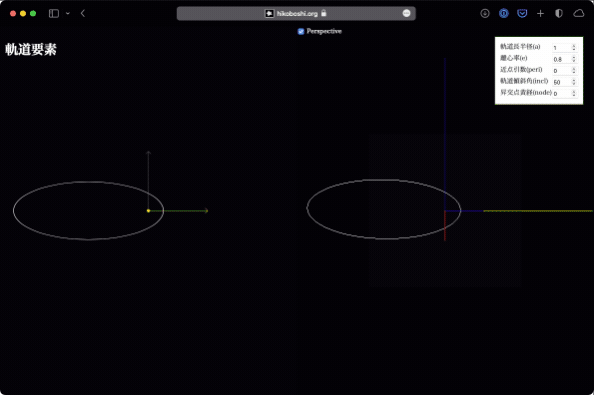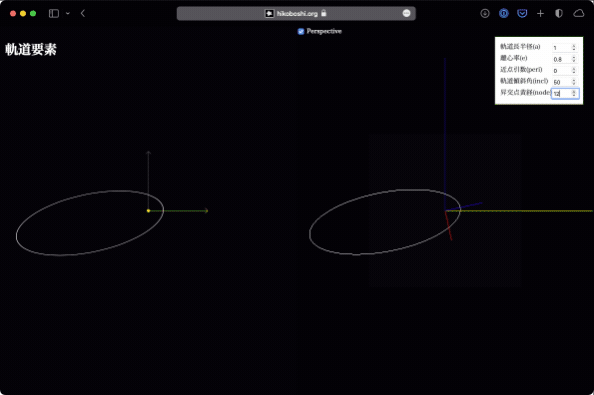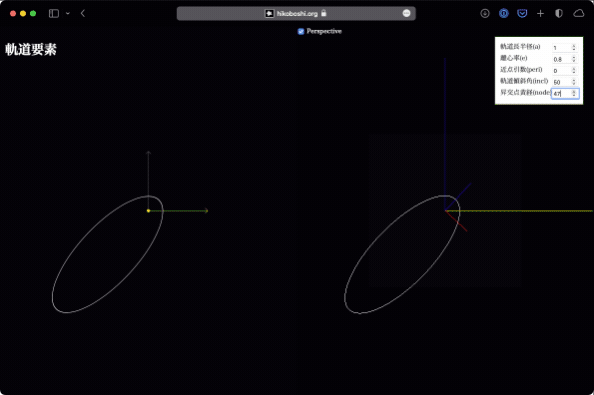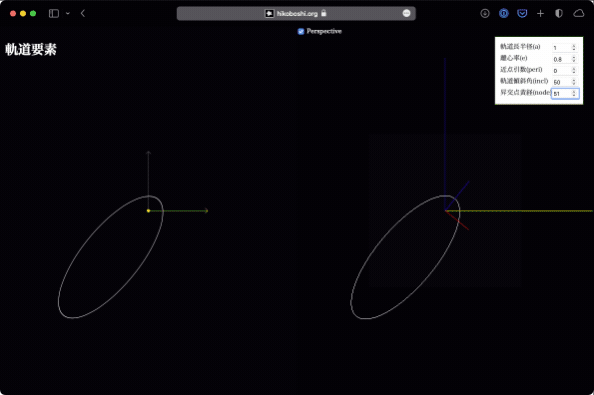
昇交点黄経

昇交点は、黄道面を南側から北側（下から上）に横切る点です。軌道傾斜角が存在すれば、黄道面をどこかで横切っているはずで、そのうちの片側になります。

昇交点黄経は、この昇交点方向と春分点方向（つまりX軸）との成す角です。逆に言えば、前述の軌道傾斜角は、この昇交点黄経を基準にした回転ということもできます。

これが変化するとはどういうことかというと、太陽を通る黄道面に垂直な方向（つまりZ軸）を軸として、軌道全体が黄道面上で回転している、という感じです。

近点引数

これはどこの角度を測っているのか…という気持ちになりますが、前述の昇交点と近点（太陽の周りを回る場合なら近日点）の成す角度です。これを動かすと、軌道平面は変わらずに軌道が回ります。

昇交点黄経の変化が、上から見たときに単純な回転に見えるのと比較すると、近点引数の変化は、軌道傾斜角がある時には少し不思議な変形をします。軌道傾斜角で指定された（斜めになった）平面上で回っているので、単純な回転に見えない、というわけです。

図を描くことについて

後半戦は、ちょこっと技術的な話になります。

今回のこの図は、平面版はSVGというマークアップ言語、立体版はJavaScriptで描いています。

前者のSVGは、XMLに基づいたマークアップ言語で、HTMLのようなものを想像していただければ良いです。イラストレータに代表されるようなベクターグラフィックソフトを使うとエクスポートできるので、ご存じの方も多いかも知れませんが、中身はXMLなので、手書きでも書くことができます。

これを用い、軌道そのものを「SVGの楕円要素」= <ellipse> タグを用いで描いています。このため、離心率が1以上の、放物線軌道や双曲線軌道は描けない、というわけです。

つまり平面版の図は、ウェブで大変馴染みのある、HTMLっぽいものだけで描いているわけです。具体的にはこんな感じ。

<ellipse
  :cx="- f * a * e"
  :cy="0"
  :rx="f * a"
  :ry="f * a * Math.sqrt(1 - Math.pow(e, 2))"
  :transform="`rotate(${-node}) scale(1.0, ${Math.cos(incl/180 * Math.PI)}) rotate(${-peri})`"
  fill="none"
  stroke="#375082"
  stroke-width="1"
  />

SVG側で軌道を表すコードは、本当にこれだけで全てです。fは大きさ調整用のスケールファクタ、a, e, node, incl, periが前述のそれぞれのパラメータです。ところどころにマイナスが入っているのは、軌道要素が右手形なのに対し、SVGの座標系が「下方向が+y」になっている左手系だからです。

ポイントになるのは、昇交点黄経、軌道傾斜角、近点引数をどうするかというところ。これはtranslateのところで表現していて、こんなふうに書いてあります。

rotate(${-node}) scale(1.0, ${Math.cos(incl/180 * Math.PI)}) rotate(${-peri})

SVGのtransformは複数を順に適用できます。このうち「軌道傾斜角」だけが少し特殊で、真上から見た時のX軸周りの回転は、形状がX軸を含む平面上にある限りは、上下方向のスケーリングに見做せます。本当に？と思いますが、立体版は実際に立体的に回しているので、同じような結果になることが確認できると思います。

思ったよりもずっとシンプルではないでしょうか（全ソースコードはこちら）。今回は、動的に動かすために若干（フォームの入力が各パラメータに反映されるような）工夫がされていますが、SVGは手書きでも十分に書けたりします。誰でも簡単に、図とかが作れそうな気持ちになったでしょうか。

ちなみに立体版は、数式から軌道上の点をたくさん作って線で結び、各種の回転変換を加える、という、想像通りのごく一般的なコードになっています。コードの大半（ほとんど全て）は立体版のためのものです。

ステラナビゲータとの比較

ステラナビゲータの「小惑星」ダイアログでは、新しい天体を加えて、好きな軌道要素を入力し表示させることができます。これで、図が正しいか確認してみましょう。

ステラナビゲータ１１

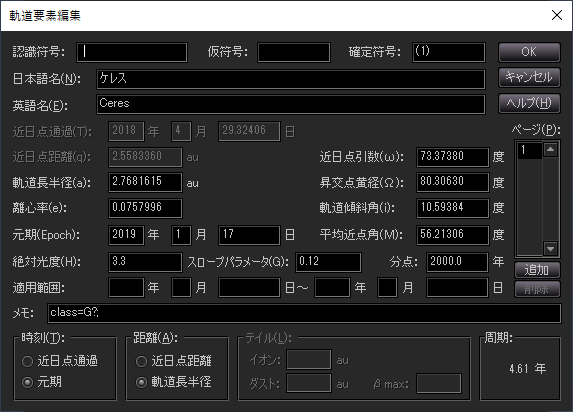
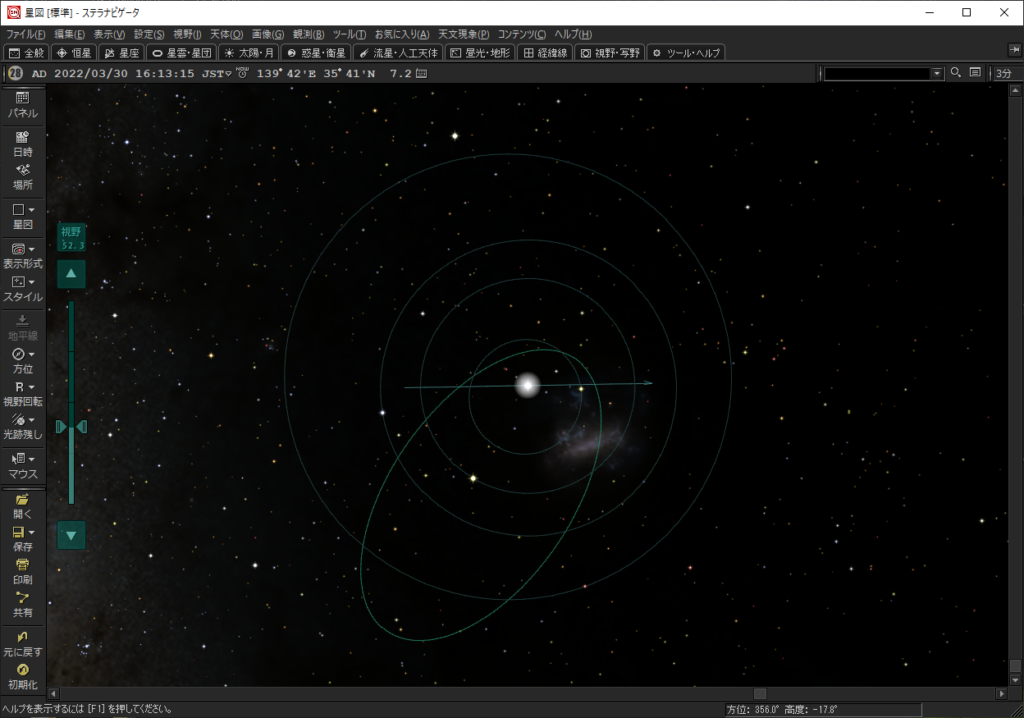
どうでしょう、よさそうですよね…？

うん？ほんのちょっと、潰れ方が違う気がする、でしょうか。気付いてしまったか…鋭い指摘です。

実は立体版と平面版も、よーく見比べると、ごく僅かに潰れ方が違う気がします。「大きさはたまたまなので置いておくと、感覚的には平面版がほんのちょっと細長いような…。その点、形状としては立体版とステラナビゲーターは似た表現のような気がします。

動いていると気付きやすくて、前述の「近点引数」のところのアニメーションをよく見てみてください。何か動きが少し違う気がしませんか。

これは立体版では遠近も表現されている（パースがかかっている）からです。ほんとに？ということで、立体版を遠近法無しで表示させたものと比較してみましょう。

ね、この微妙な差、どうやら遠近のせいらしいでしょ。無しにすると、平面版と立体版は、形状もほぼ一致すると思います（サイズが一致するのはたまたまです）。

この図であれば、軌道の左下側がカメラから遠い、というわけ。遠近法を無しにすると、余計な歪みが生まれないのは良いのですが、立体感が若干掴みにくくなります。

まとめ

一見混乱しそうなパラメータのセットであっても、パラメータに応じて動かせると理解が進みやすいです。SVGはXMLなので、「何かの画像ソフトで作る」というだけでなく、手書きでも案外いろいろ描けて便利です。やってみてね。

おまけ

今回は軌道要素を動く図にしてみましたが、ステラナビゲータを使っていると、ちょこちょこと軌道要素が更新されていることにお気づきかもしれません。よくみるとステラナビゲータの軌道要素データには有効期間に関する記載があって、ものによっては一つの天体に複数の軌道要素が設定されていたりもします。

新天体であれば観測が進んで精度が上がるなどの事情、彗星とかであればガスの噴出等で軌道が変わってしまうと言った事情もありますし、太陽以外の天体（太陽系内であれば大きいのは木星）の影響を受けて軌道が変わる（摂動）といった事情も出てきます。美しい数式で定義できれば素敵ですが、現実には適時更新していく必要がある、ということです。