最近、「プログラミング教育」という言葉をよく耳にするようになりました。小学生のうちからプログラミングに親しむ、今はそんな時代なんですね。先日、姪がプログラミング学習用のWEBサイトで楽しそうに何か作っているのを見て、これで何かやってみようと考えたのが今回のお題です。題して「Scratchで天文計算」シリーズ。第1回では、ハレー彗星が太陽の周りを回る様子を計算するプログラムを作ってみましょう。
Scratchをはじめよう
Scratchは、MITメディアラボで生まれた、誰でも無料で楽しめる学習用のプログラム環境です。画面上でパズルを組み立てるようにプログラムを作ることができます。最初にWEBブラウザでアカウントを作ります。このアカウントでログインして、「作る」というボタンをクリックすると次のような画面が表示されます。
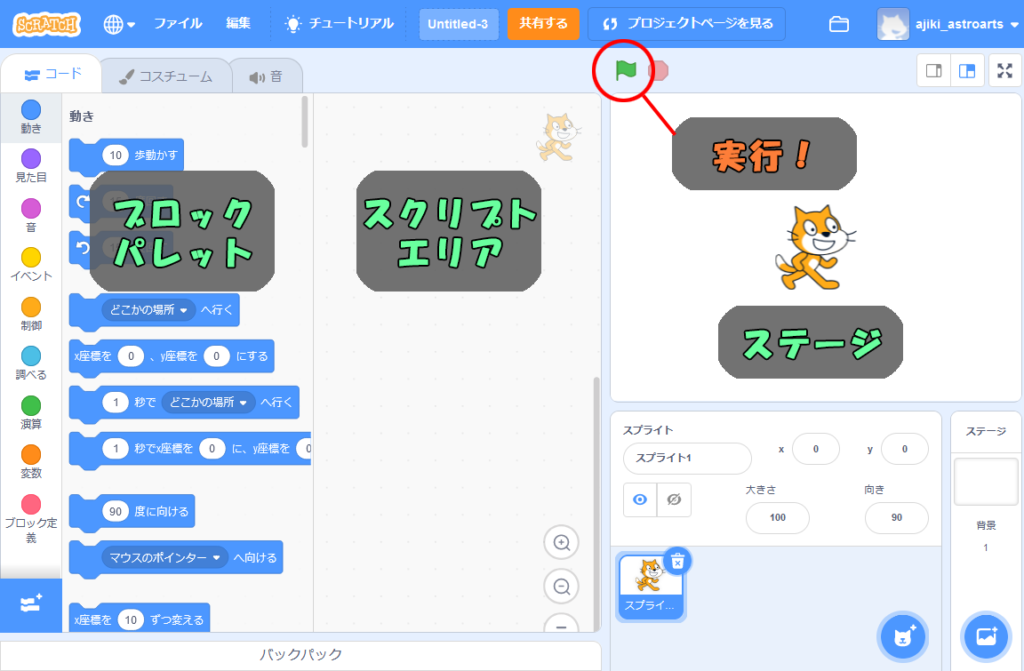
左側の「ブロックパレット」にならんでいる部品を選んで、中央の「スクリプトエリア」に並べていくだけでプログラムを作ることができます。作ったプログラムを実行した結果は、右上の「ステージ」に表示されます。
初めてのプログラム
さっそくプログラムを作ってみましょう。Scratchのプログラムは、「ステージ」の上にある緑色の「旗」のマークをクリックすると実行が始まります。そこで最初は、ブロックパレットの「イベント」のグループにある「旗が押されたとき」をマウスでドラッグしてスクリプトエリアに置きます。

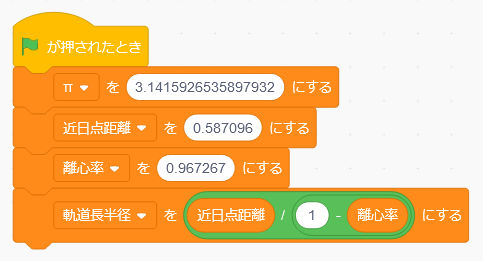
さて、天文の計算ではたびたび円周率πが出てきますので、まずはこれをプログラムに書いておきましょう。Scratchでは「変数」を作って、ここに数字や文字を入れておくことができます。まずブロックパレットの「変数」のグループにある「変数を作る」をクリックします。
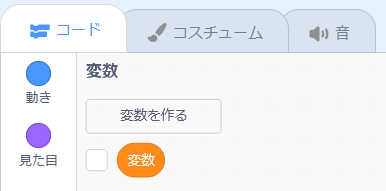
ここで表示されるウィンドウで、「π(パイ)」という名前をつけて新しい変数を作ります。
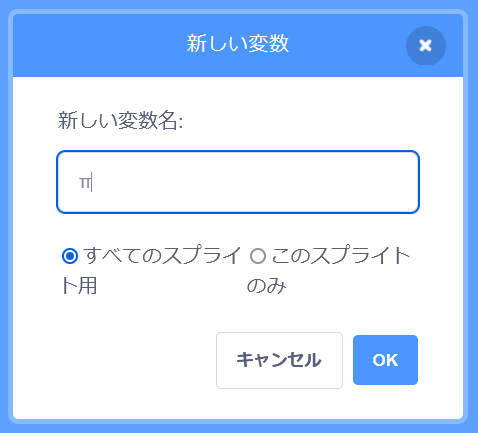
次に先ほど配置した「旗が押されとき」の下に、「変数を〇にする」というブロックを置いて、変数「π」に円周率を入れてみましょう。ここでは、あとで使えるように精度の高い数字「3.1415926535897932」を入れおきます。
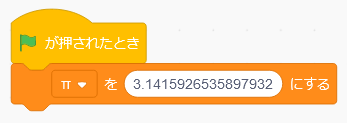
さあ、最初のScratchプログラムの実行です。旗をクリックすると、「ステージ」には次のように表示されます。
変数「π」には、ちゃんと円周率が入っていることがわかります。
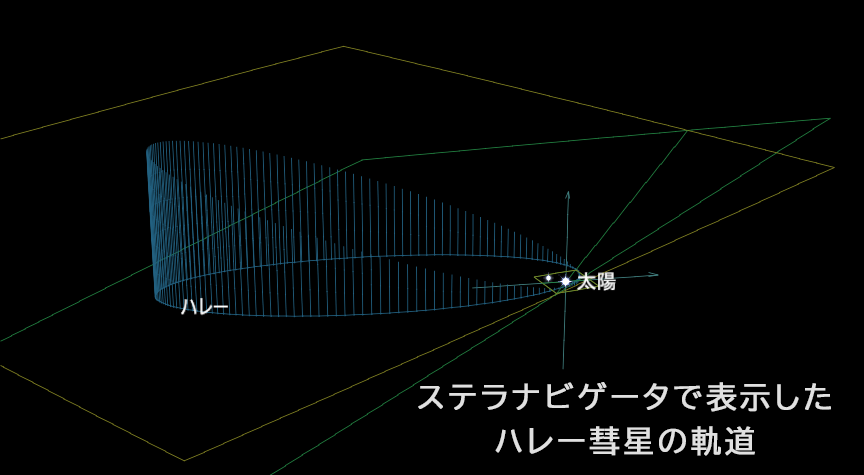
彗星の軌道を表すパラメータ
ここからは、ハレー彗星についての情報を変数に入れておくことにしましょう。彗星に限らず、太陽の周りを回る天体の軌道を表すには、いくつかのパラメータが必要です。
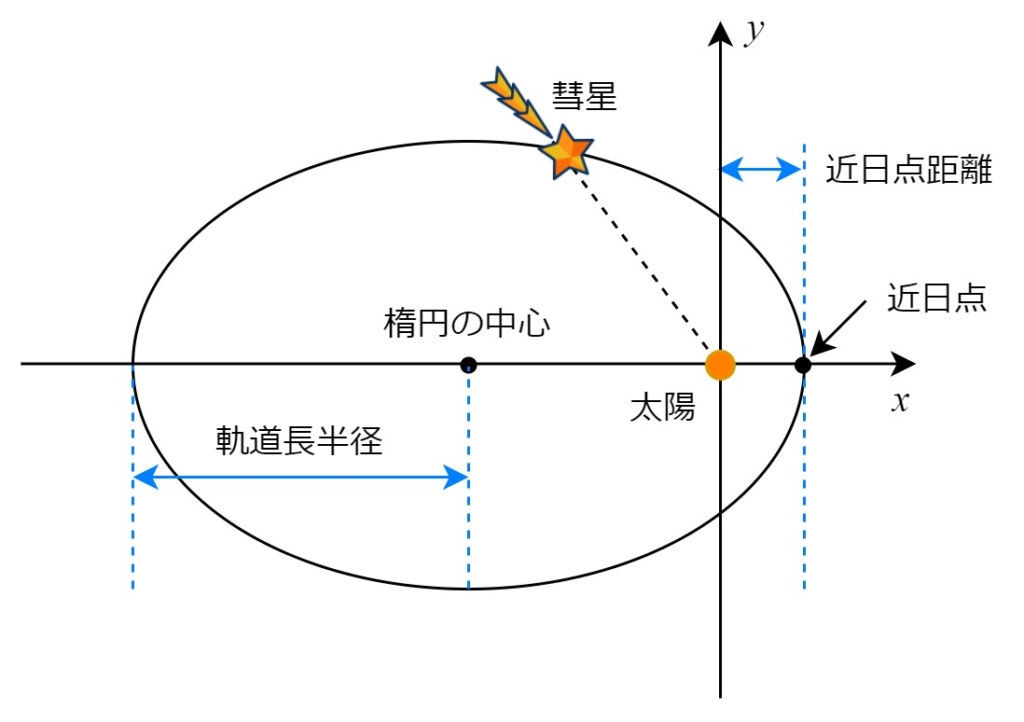
- 近日点距離
彗星が太陽に一番近づく場所を「近日点」、その点の太陽からの距離を「近日点距離」と言います。ふだん使うキロメートルのような単位を使うと「何億km」のようなすごく大きな数字になってしまうので、太陽と地球の間の距離を1とした数で表します。この単位を「天文単位」といい、auと書きます。つまり、地球から太陽までの距離は1auです。
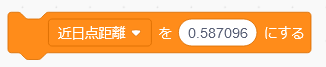
ここでは、「近日点距離」という変数を作って、ハレー彗星の近日点距離である0.587096を入れておきましょう。この数字からわかるように、ハレー彗星が太陽に一番近づいたときの太陽との距離は、地球と太陽の距離の半分ほどです。
- 離心率
彗星は太陽の周りを楕円を描いてまわっています。この楕円がどれくらい細長いかを表すのが「離心率」です。離心率がゼロの場合は円軌道、数字が0.1、0.2のように大きくなっていくにしたがって細長い楕円になり、1.0になるともはや楕円ではなく、再び太陽のそばに戻ることのない開いた曲線(放物線)になってしまいます。
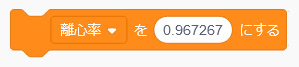
ハレー彗星の軌道はとても細長い楕円形をしていて、離心率は0.967267です。これを変数「離心率」に入れておきましょう。
軌道の大きさを計算しよう
次に一つ計算してみましょう。上記の2つの数字がわかると、ハレー彗星の細長い楕円軌道の長さの半分(軌道長半径)がわかります。
軌道長半径は次のようにして計算できます。
軌道長半径 = 近日点距離 ÷ (1 – 離心率)
これをScratchのブロックにすると、こうなります。

さて、ここまでのブロックを全部つなぐとこうなります。
さあ、実行してみましょう。
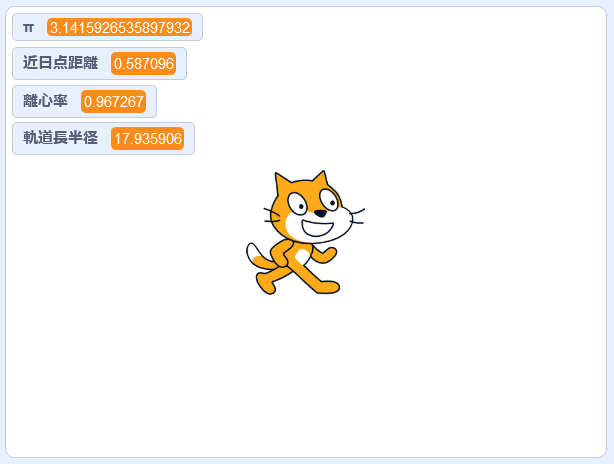
軌道長半径が計算されて、17.935906と表示されています。これは半径なので、楕円の長さはその2倍の約36auということになります。これはau、つまり天文単位ですから、ハレー彗星の楕円軌道の長さは、地球から太陽までの距離の約36倍もあるということです。
先ほどの軌道の図を見ると、ハレー彗星が太陽に一番近づいたときの「近日点距離」は0.587096でしたから、軌道長半径(軌道の長さ)から近日点距離を引くと、彗星が太陽から一番遠ざかったときの距離、つまり「遠日点距離」がわかります。
遠日点距離 = 17.935906 * 2 – 0.587096 = 35.284716au
海王星の軌道の半径は約30.1auなので、ハレー彗星は海王星よりも遠くまで行くことになります。
ここまでのプログラムを Scratch ハレー彗星1 に置いておきます。
次回は、実際にハレー彗星がどんな動きをするのかを調べてみることにします。