前回までで、ハレー彗星の楕円軌道を表示することができました。このプログラムでは、軌道の形は正しいのですが、実は彗星が動くスピードが実際とは違っていて、ハレー彗星の場所による速度の違いが再現できていません。彗星は太陽に近い時には速く、太陽から遠ざかるとゆっくりと動いています。今回はこれを考慮して、速度の変化まで正しく計算することにしましょう。
前回の記事「【Scratchで天文計算】第3回 軌道の図を描いてみよう」はこちら
ハレー彗星がまわる周期
さて、ハレー彗星は約76年かかって太陽の周りを一周すると言われていますが、まずはこの周期を計算で求めてみましょう。これには次の式を使います。
公転周期(年) = 1.00004024 × 軌道長半径 × √軌道長半径
さっそくScratchで計算してみましょう。前回のプログラムで軌道長半径を計算した後に次のようにします。

実行してみると、「公転周期 75.963058」と表示され、ハレー彗星の公転周期が約76年という話と一致します。
平均日々運動と平均近点角
もう一つ必要なパラメータがあります。ハレー彗星が約76年をかけて、毎日一定の角度で太陽の周りを一周すると仮定して、一日あたり何度ずつ回るのかを表す「平均日々運動」という値です。これは次のようにして計算します。
平均日々運動(度/日) = 360 ÷(公転周期 × 365.2422)

前回のプログラムでは、離心近点角を0から360まで繰り返してハレー彗星の位置を計算していました。今回は、離心近点角ではなく、「平均近点角」という角度を使って位置を計算します。ハレー彗星が近日点にいる時の平均近点角は0度です。ここから1日経過するごとに平均近点角は「平均日々運動」の分だけ増えていき、再び太陽に最も近い位置に戻ってきたときには360度になります。この平均近点角から離心近点角を計算し、あとは前回と同じようにして位置を求めるという流れになります。
日数を使って計算しよう
ここで、平均近点角を0から360まで繰り返すことでもハレー彗星の楕円軌道を計算できるのですが、今回は時間を基準にして計算しようと思います。最初は太陽に最も近づいたときから始めて、そこから15日おきのハレー彗星の位置を計算します。つまり、日を0から初めて15日後、30日後、45日後、のように進めていきます。前回のプログラムを書き換えると、次のようになります。
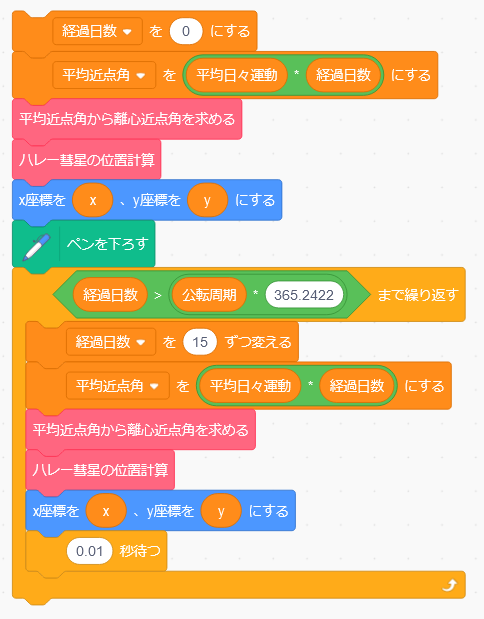
このプログラムでは、ハレー彗星が太陽に最も近い位置を通過してから何日が経過したかを「経過日数」という変数に入れています。最初は0です。この経過日数に平均日々運動をかけるとその日の平均近点角になり、そこから離心近点角を求められれば、あとは前回と同様に離心近点角からハレー彗星の座標を計算できます。
計算の繰り返しは、ハレー彗星が近日点にある時から、太陽のまわりを一周して戻ってくるまでです。すでにハレー彗星の公転周期は計算しましたが、この公転周期の単位は「年」でした。今は日数で計算しようとしているので、これを「日」の単位にします。うるう年もあって1年の長さは年によって変わりますが、平均は365.2422日です。よって、(公転周期×365.2422)が日の単位であらわした公転周期であり、経過日数がこの日を超えるまで繰り返すようにします。
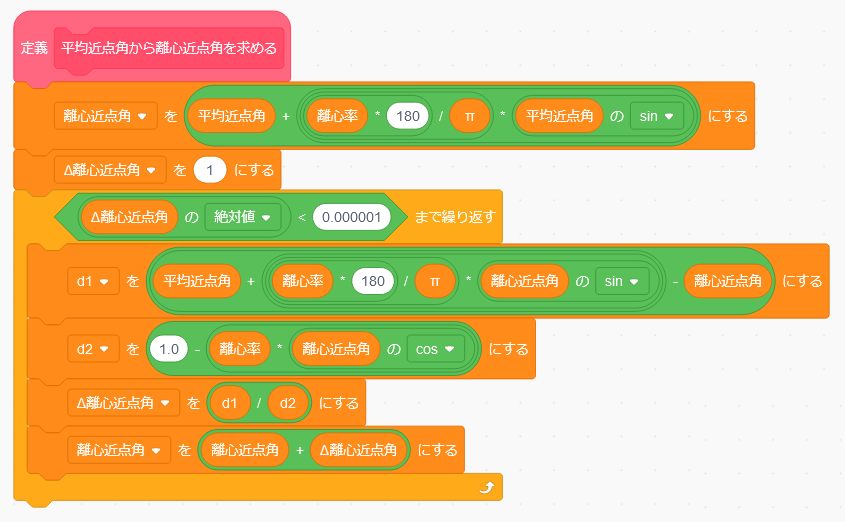
平均近点角から離心近点角を求める
ここで、「ハレー彗星の位置計算」というブロック定義を呼び出す前に「平均近点角から離心近点角を求める」というブロック定義を呼び出しています。次は、この平均近点角から離心近点角を求めるブロックを作っていきます。
平均近点角と離心近点角は、次の式ような関係にあります。
平均近点角 = 離心近点角 - 離心率 × sin(離心近点角)
これを「ケプラー方程式」と言います。この式を見てわかるように、離心率は定数ですので、離心近点角がわかっていれば平均近点角を求めるのは簡単です。しかし、今は逆に平均近点角から離心近点角を求める必要があります。残念ながらこれを簡単に求める方法はありません。そこでプログラミングの出番です。
ケプラー方程式を解く
まず、ケプラー方程式は角度をラジアンで計算するようになっているのですが、Scratchでは度の単位を使うため離心率に(180/π)をかけておきます。これによって先ほどのケプラー方程式は次のようになります。
平均近点角 = 離心近点角 - 離心率 × (180/π) × sin(離心近点角)
次に、この式を変形します。
離心近点角 = 平均近点角 + 離心率 × (180/π) × sin(離心近点角)
この式で離心近点角を求めますが、右辺にも離心近点角があり、この値はわかりません。そこで、かわりに離心近点角と大きくは変わらないであろう平均近点角を入れて、離心近点角の近似値を計算します。

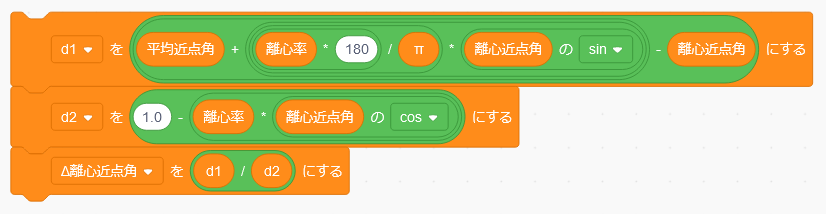
これは、求める離心近点角に近いかもしれませんが、さらに正しい離心近点角に近い値を求めるため、次のようにして「Δ離心近点角」を計算します。
d1 = { 平均近点角 + 離心率 × (180/π) × sin(離心近点角) }× 離心近点角
d2 = 1 - 離心率 × cos(離心近点角)
Δ離心近点角 = d1 ÷ d2
ここで使う離心近点角は、上で求めた近似値です。これをScrachにすると次のようになります。
さきほどの離心近点角の近似値に「Δ離心近点角」を加えると、より正しい値に近い離心近点角が求められます。この新しい離心近点角を使って、もう一度上の式で「Δ離心近点角」を求めて離心近点角に加え…ということを繰り返していくことで、どんどん正しい離心近点角に近づけていくことができます。繰り返していくうちに「Δ離心近点角」がある程度小さくなったら十分正しい値に近づいたとみなし、繰り返しを終わります。
ここまでをまとめると、ブロック定義「平均近点角から離心近点角を求める」は次のようになります。
これで全部そろいました。完成したプログラムを実行してみましょう。
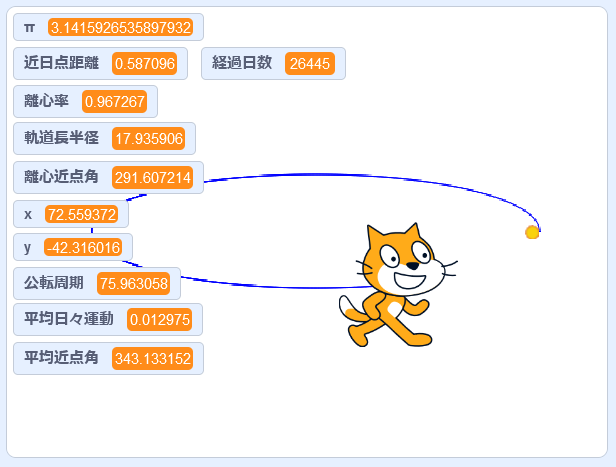
ハレー彗星が太陽から遠くなるにしたがって動きがとてもゆっくりになるのがわかると思います。
ここまでのプログラムを Scratch ハレー彗星4 に置いておきます。
さて、ハレー彗星が楕円軌道を描いて、太陽に近いときは速く、遠くなるとゆっくりと動くことはわかりました。前回ハレー彗星が太陽に近づいたのは1986年のことです。そこからどんどん太陽から遠ざかるのですが、今回のプログラムでは、何年何月何日にどのあたりを通るのかはわかりません。そこで、次回は日付もわかるようにしたいと思っています。お楽しみに!