前回のハレー彗星の軌道の大きさの計算はできたでしょうか。今回は、ハレー彗星の位置を計算してみましょう。
前回の記事「【Scratchで天文計算】第1回 ハレー彗星を計算しよう」はこちら
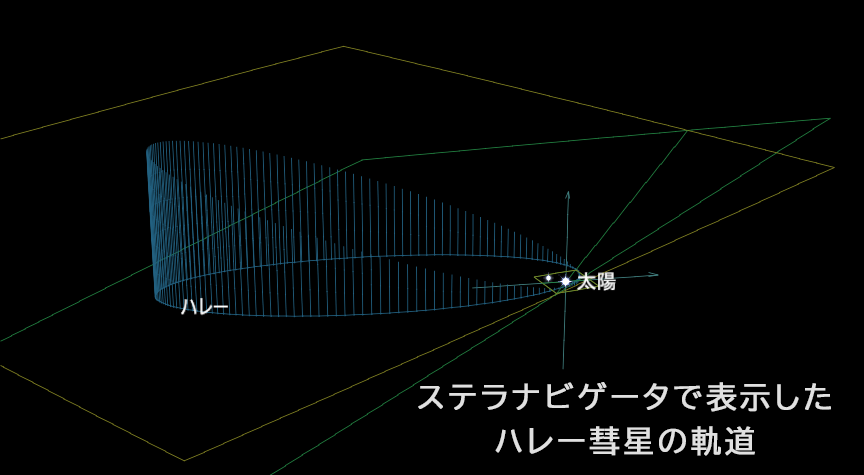
位置計算のための座標
まず座標の原点を太陽におきます。原点の右方向に近日点があり、彗星が反時計回りにまわるものとして、右に向かってX軸をプラス、Y軸を上方向にプラスで表します。もちろん距離の単位はau(天文単位)です。前回も示した次の図は、このような座標系を図示したものです。
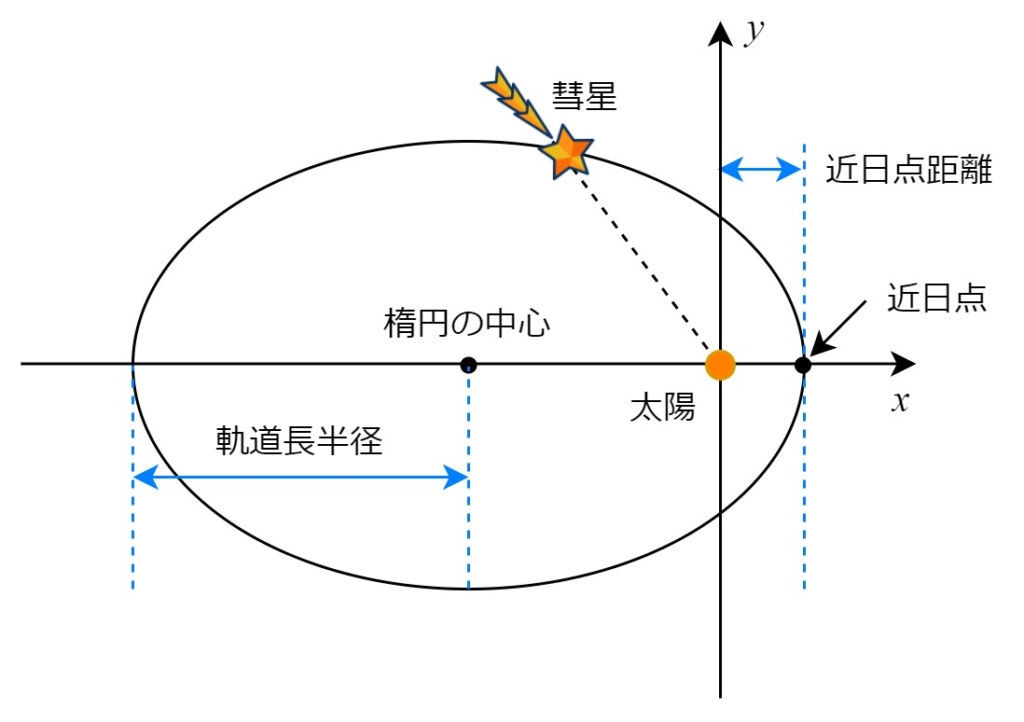
太陽を中心に計算するのは難しい
太陽から見て近日点の方向を0度とし、彗星は太陽の周りを反時計回りに360度まわって近日点に帰ってきます。この彗星の動きを直接調べようとすると計算が複雑になるので、今回は次の図のように考えます。
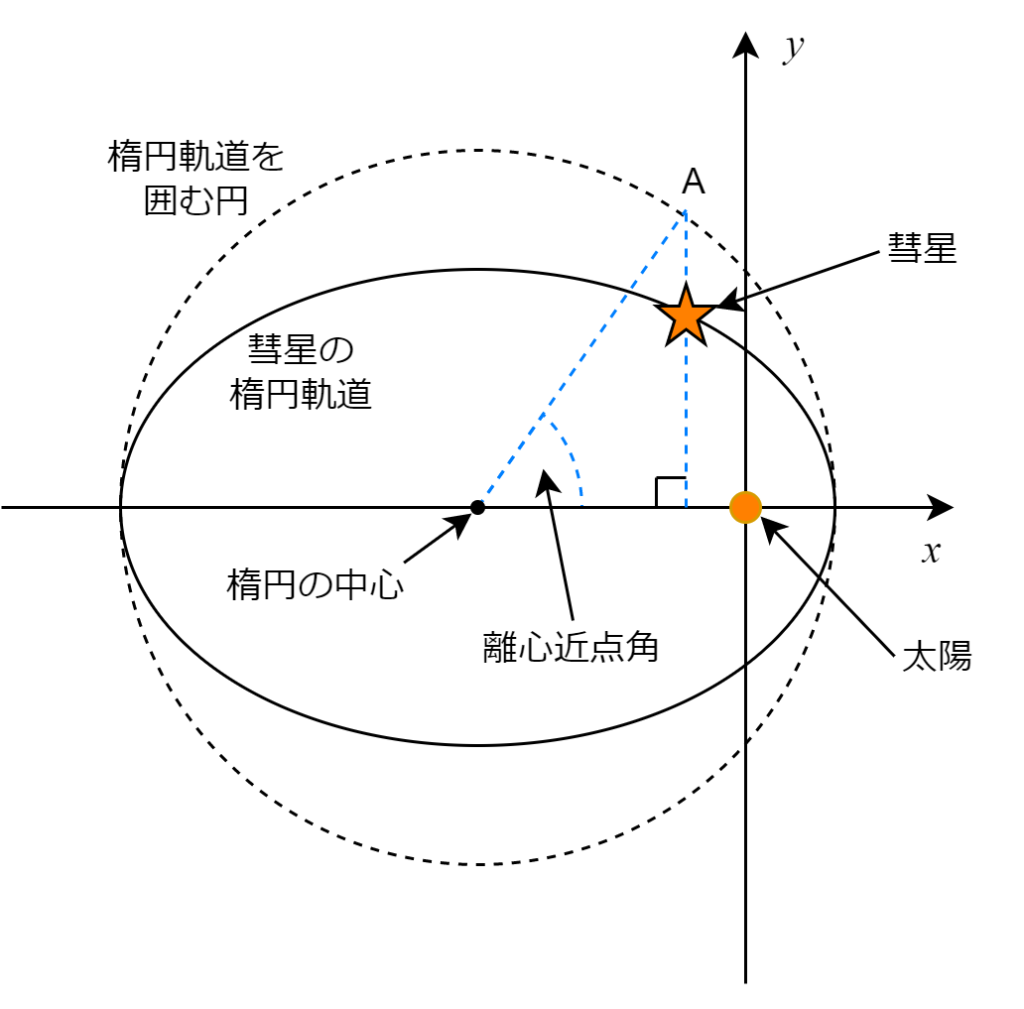
この図では、彗星の楕円軌道をかこむように点線で円を描いています。ここで、楕円軌道上にある彗星から縦に直線をひき、この線が先ほどの点線の円と交わる点Aを考えます。この点Aと楕円の中心を結んだ線を考え、これがX軸と交わる角度を「離心近点角」と言います。彗星が楕円軌道上のどこにあるときでも唯一の離心近点角が決まり、逆に離心近点角を決めれば彗星が楕円軌道上のどこにあるかが決まります。
彗星が、ある特定の離心近点角の場所にあるときに、太陽を原点とした彗星の座標(x,y)は次のようにして計算できます。
離心近点角を使ったプログラム
x = 軌道長半径 × { cos(離心近点角) – 離心率 }
y = 軌道長半径 × { √(1 – 離心率 × 離心率) × sin(離心近点角) }
さあ、Scratchで変数xとyを作って、これを計算してみましょう。もちろん計算に使う離心近点角は、変数「離心近点角」に入れておきます。なお角度の単位は、多くのプログラミング言語で「ラジアン」を使うのに対して、Scratchでは「度」を使うので注意してください。

前回のプログラムも含めて、ここまでのブロックを全部つないで実行してみましょう。
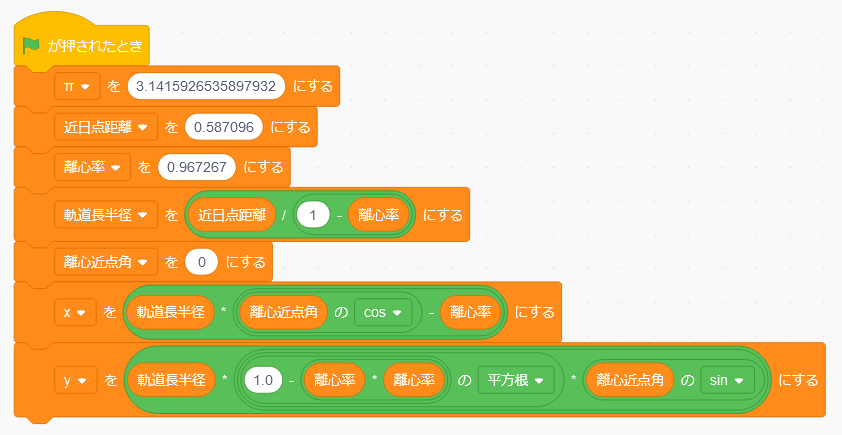
結果は次のようになります。
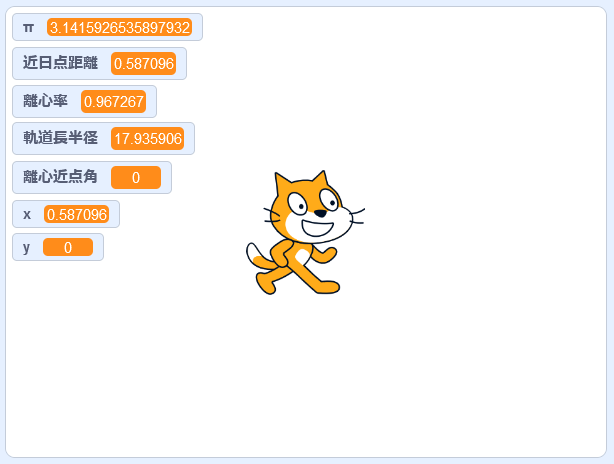
さきほどの軌道の図で考えると、離心近点角が0度になるのは、彗星が太陽の右側、x軸上にあるときですね。このとき、太陽から彗星までの距離は「近日点距離」と同じ0.5870976auで、これがそのままX座標になり、Y座標は0です。先ほどの画面に表示されている数字は、これに一致していることがわかります。
彗星が軌道をまわるプログラム
さて、せっかくプログラムを作っているのですから、離心近点角が0度のときだけでなく、0度から360度まで変わっていくときに、ハレー彗星の座標(x,y)がどのように変化していくのかを調べてみましょう。
そのためこの(x,y)の計算を、離心近点角を0から360まで変えながら繰り返します。これにはScratchのブロックパレットの「制御」のグループにある「まで繰り返す」というブロックを使います。最初は離心近点角を0にした後にこの繰り返しブロックをおいて、その繰り返しの中にx,yの計算を入れます。

離心近点角を0度からはじめて360度を超えるまで繰り返すので、繰り返しの条件を考えると「離心近点角 > 360 まで繰り返す」になります。

このままでは離心近点角が変化しないのでいつまでたっても0のままです。よってx,yの計算結果も変わらず、繰り返しが終わることもありません。そこで、繰り返しの中で離心近点角を1度ずつ変えることにします。
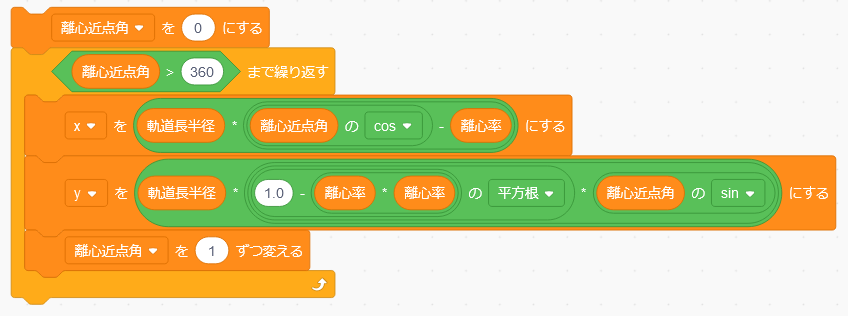
さあ、これで実行してみましょう。結果は次のようになります。
プログラムをゆっくり動かす
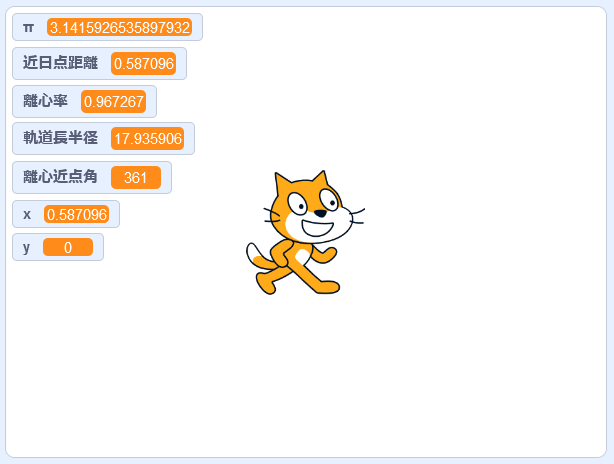
離心近点角を0から360まで繰り返すはずだったのですが、一瞬にしてプログラムが終わってしまいます。画面を見ると離心近点角は361になっていて、たしかに繰り返しが終了する条件が成立していることがわかります。実は、プログラムの実行が速すぎて、すべてが一瞬のうちに終わってしまったようです。そこで、繰り返しの中に時間待ちを入れてみることにしましょう。ここでは0.01秒ずつ待つことにします。
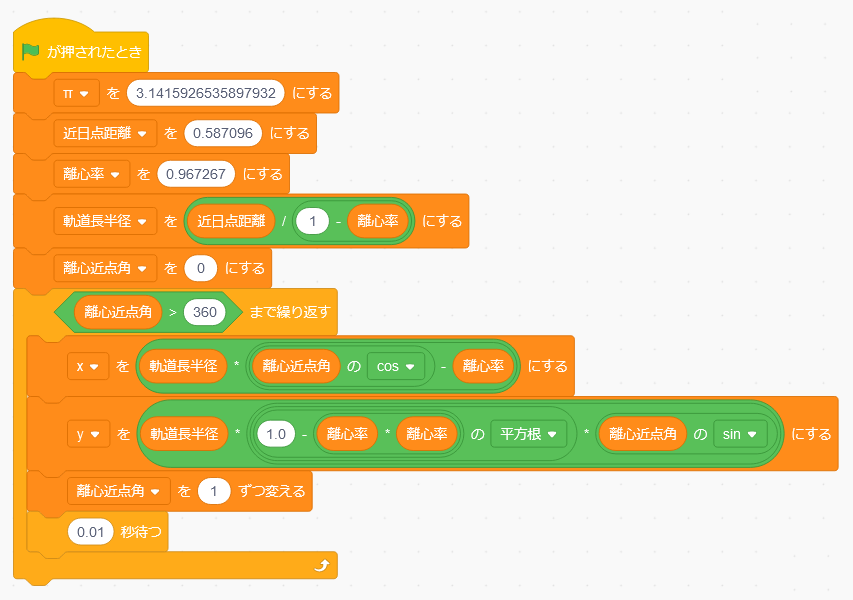
これで実行すると、離心近点角が1ずつ増え、それにしたがってxとyが変わっていく様子を見ることができます。最初は離心近点角が0ですから彗星が近日点にある状態から始まります。はじめのうちはx,yともに正の数なので、太陽の右上を反時計回りに動いていきますが、xが次第に減少してマイナスになるので、太陽の左上に移動していくことがわかります。さらに時間がたつとyが減少してマイナスの数、つまり太陽の左下に移り、つづいてxが増加してプラスの数字になると太陽の右下、最後は近日点に戻ってくるのがわかります。
ここまでのプログラムを Scratch ハレー彗星2 に置いておきます。
さて、これで数字が変わるのは分かりますが、頭の中で座標からハレー彗星の動きを想像するのは難しいかもしれません。そこで次回は、今回計算したハレー彗星の座標を使って軌道を図にしてみます。