プラネタリウム事業部のとよだです。以前、軌道要素の可視化について書いてみたのですが、そのあと安喰さんによるScratchで天文計算するものも登場しました。一見難しそうなお話ですが、見てみると面白いです。
軌道要素の可視化:動く説明図を作りました 太陽系の周りの天体の動き(小惑星や彗星など)は、実はシンプルな式で表せてしまうんです!式の中の変数を変えることで小惑星の動き方が身近に感じられるかも!
【Scratchで天文計算】第1回 ハレー彗星を計算しよう 誰でも無料で楽しめる学習アプリ「Scratch」。パズルのように組み替えることでプログラムを学んだり、ゲームを作ることもできちゃうツールです。「Scratchで天文計算」ではハレー彗星の動きを計算して動かしてみます。自由研究にもおすすめの記事です。
しかし、ただ形が知りたいだけなのにプログラミングか……みたいな時もありますよね。そこで “GeoGebra” でやってみたいと思いました。
GeoGebraとは
GeoGebraはクラウド上で使える数学アプリです。
数学アプリというと字面だけで難しそうですが、何はともあれ数式を入れたらグラフ化してくれる素敵なアプリになっています。

いじっていると1日くらい簡単に溶けるので注意が必要です(人による)。
お勉強とかに大変便利なのはもちろんですが、この数式なにやってるのかわからないなあ……なんて時にも簡単に使えてありがたいです。つまりまさに今。
ということで、軌道計算を題材にして少し理解を深めてみたいと思います。
GeoGebraにグラフを描かせよう
数式を入れる。以上。

簡単すぎて、説明できる内容がありません……。
ひとまず、中学とかでやった $$y = x$$ みたいなものを入れてみると良いと思います。早速やってみましょう。
上記の URI を開き……「アプリの開始」ボタンを押すと……何やら入力できそうな画面になります。
ちなみにウェブ版だとキーボード入力がうまく動かない場合があります(Safariなどで)。
もし「これは怪しいな」と思ったら、 Chrome などブラウザを変えたりしてみてください。
実際に数式を入れてみると……斜めの直線が描けますよね。そうそう、一次関数ってこういうのでした。恐ろしく簡単。
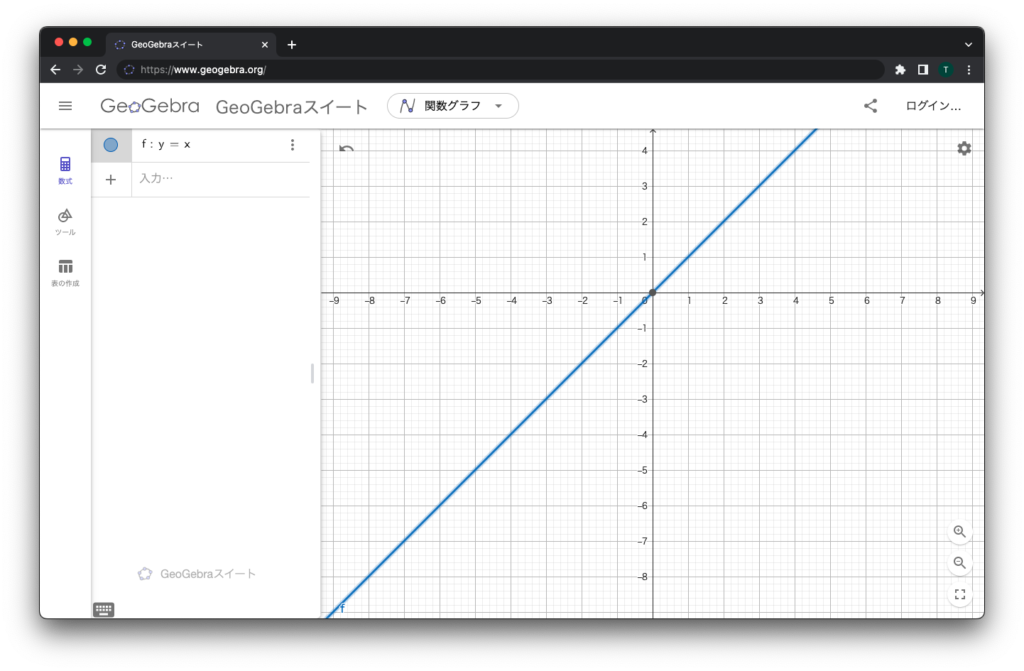
つまり、何かしら数式を入れてあげれば、グラフにしてくれるというわけです。どんどん入れてみましょう。 y = x ^ 2 とかはどうでしょうか。頭に係数をつけた y = 2 * x ^ 2 はどうでしょう。
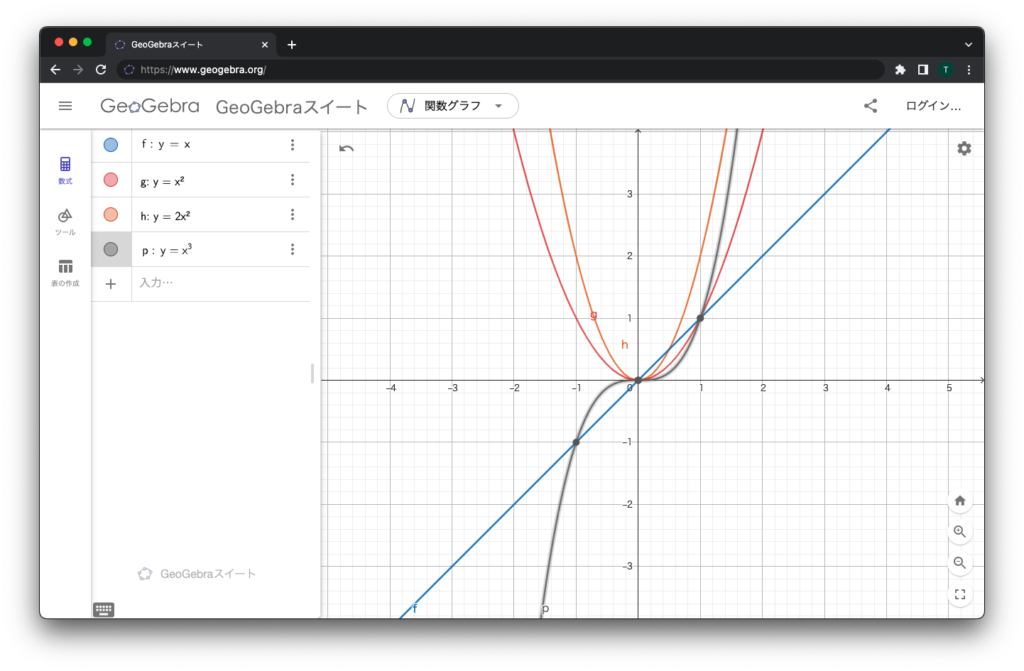
数式なんて言うと難しそうですが、ほんのちょっと何かを変えて様子の違いを見ていくと、だんだんと数式の秘密がわかってくるものです。しかもこれならとても簡単。

不思議とだんだん楽しくなってくるはずなので、とりあえず思いついたことをポンポン書き入れて遊んでみましょう。
パラメータを組み込む
数式を入力するだけで出てくるのはそれだけで便利ですが、手書きグラフより優れている点として、あとから変えることのできる「パラメータ」を仕込む、という機能があります。例えば
$$y = a ( x – b ) ^ 2 + c$$
のようなものを考えてみましょう。

この数式では、 a, b, c が「パラメータ」です。
GeoGebra では、パラメータらしきものがあると勝手に定義してくれるので、 y = a ( x – b ) ^ 2 + c をそのままコピペしてみてください。
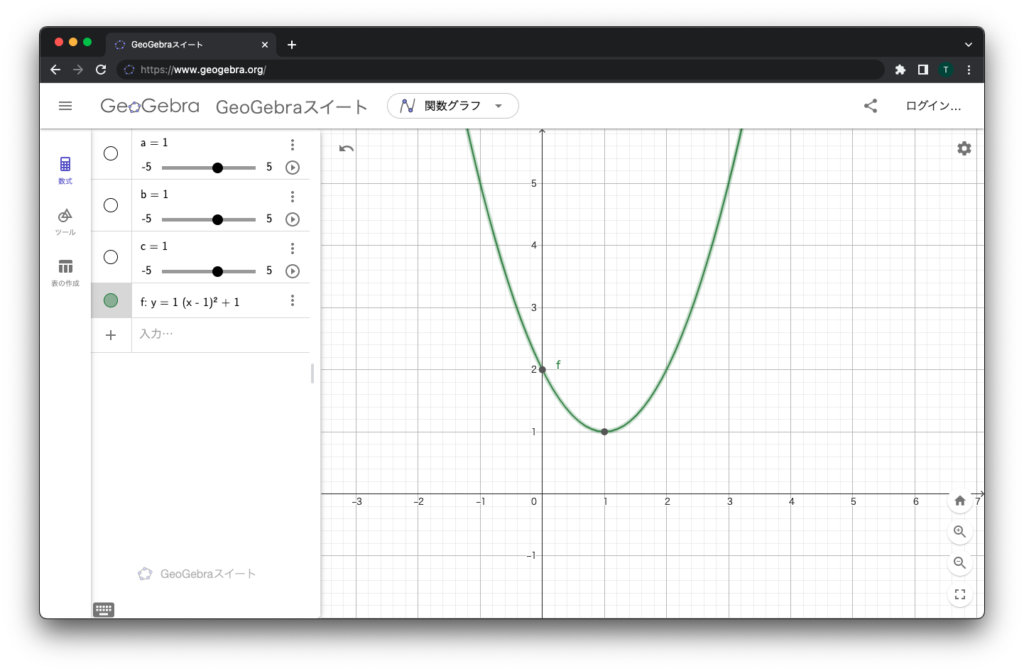
a, b, c が勝手に定義されて、スライダーが作られました(図左側)。

a を変えるとなだらかさが、 b を変えると横方向(x軸方向)の位置が、cを変えると縦方向(y軸方向)の位置が変わると思います。
このように、数式を少し変えながら様子を見ることができると何かと発見があって、数式に関する理解を深めることができます。
軌道の形を描く
さて、 GeoGebra の面白さを知ったところで、軌道の形を描かせてみましょう。
以前の記事では、軌道の「形」と「傾き」を決定している幾つかのパラメータを紹介しました。今回はその中でも、「形」を決めている「離心率」と「近点距離」を考えたいと思います。
ここからは少し複雑な数式が出てきます。

アレルギーのあるかたは「ああそれそれ!」とわかったふりをしながら、心を無にしてコピペしてOKです。
理解の有無に関わらず数式を絵にできるところが GeoGebra の素晴らしいところ。絵になってから弄ってみれば逆に数式が少しわかってきますので、最初から納得できる必要はありません。
①まず最初に、ちょっとした都合から、 GeoGebra に先にパラメータをお伝えしておきます。
e = 1
q = 1これを一つずつコピペするとスライダーが出てきます。
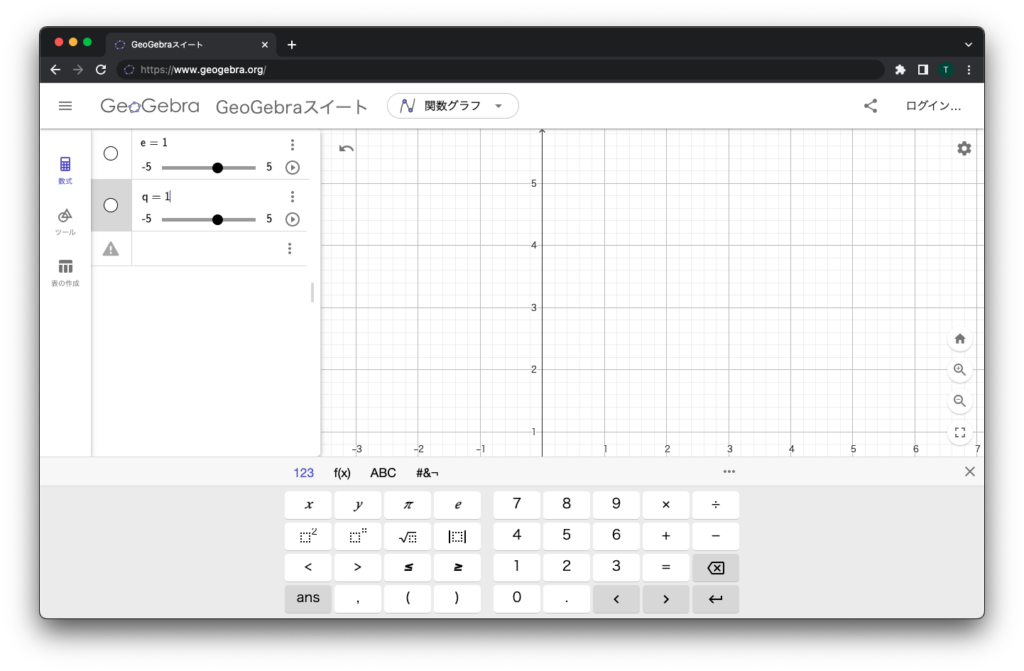
ちなみに e が「離心率」、 q は「近点距離」のことです。自動で出てくるスライダーだと、 -5 から 5 の範囲になっていますが、離心率も近点距離もマイナスになったらちょっと変なので、設定だけ変えておきましょう。
②数式の右にある点々をクリックして、「設定」を選びます。「スライダー」のタブをクリックして、「最小」を 0 に、「最大」を2あたりにして、「増分」も0.01など細かくしておいてください。
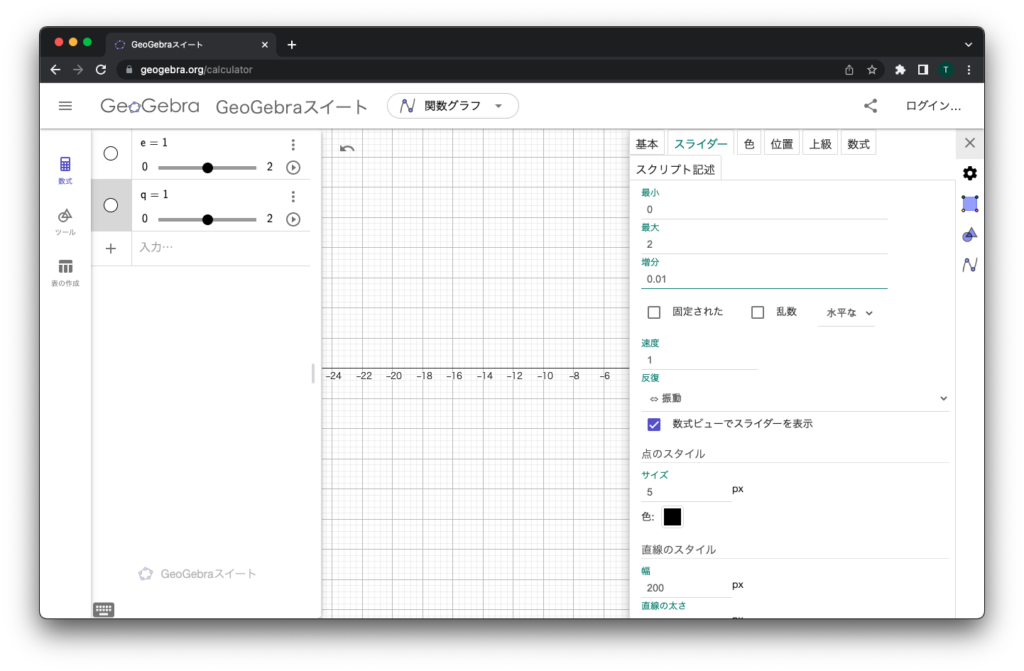
③次は軌道の形を決める数式です。「二次曲線」という数式で、こういうものですが
$$r(\theta) = \frac{q (1 + e)}{1 + e \cos\theta}$$
θは書きにくいので t に変えて、以下のような呪文(?)をコピペします。
r(t) = q ( 1 + e ) / ( 1 + e cos(t) )そうするとなんだか変な形が登場します。
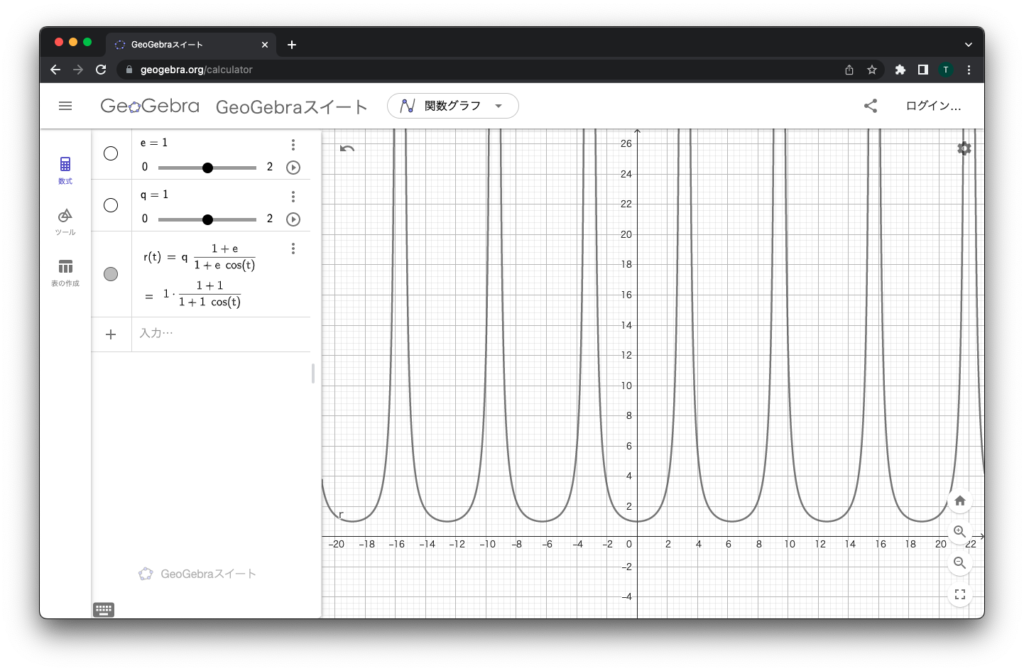
GeoGebra は頑張り屋さんなので、何でもかんでもなんとかグラフ化してくれようとします。が、この数式は「極座標」というもので作ったものなので、普通のグラフで使う「直交座標」(縦横になっている座標)で描くのはちょっと工夫が必要なのです。
数式の左を見ると、丸くて色のついている場所があります。これをポチッとクリックすると、表示・非表示が切り替えられるので、押してみてください。そうすると、いったんまっさらになります。
④最後に、極座標の関数をうまいこと直交座標に変換してあげましょう。以下の呪文で、極座標の関数を直交座標にして描かせます。
(r(t) cos(t), r(t) sin(t))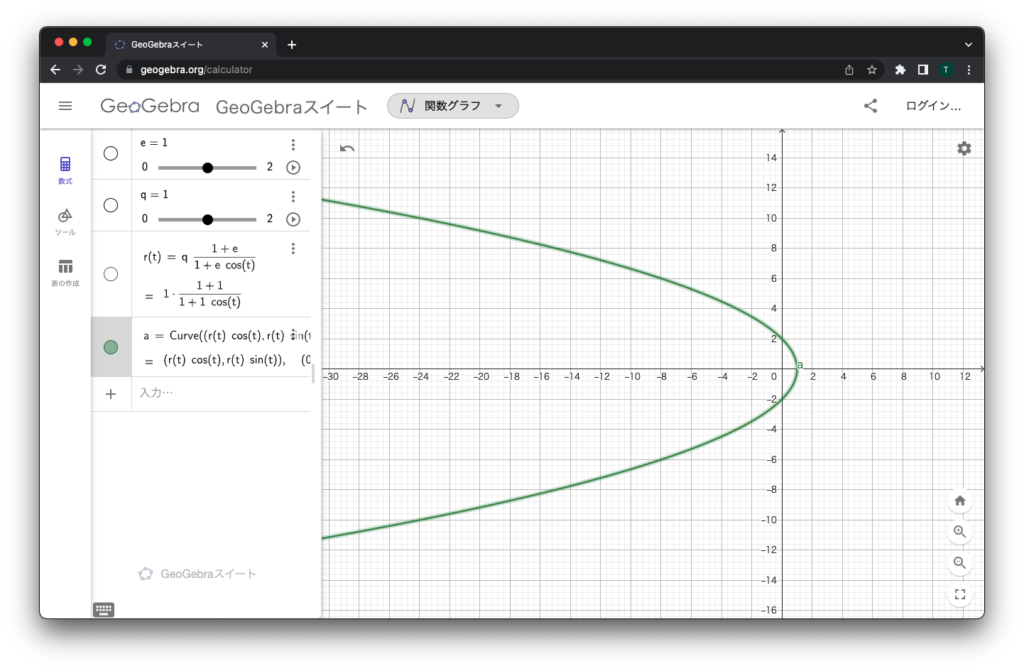

なんだかよくわからないけど、何かが描けました!
グラフをいじる
離心率を変えてみよう!
この状態で、まずは離心率 e のスライダーを動かしてみてください。とりあえず左に目一杯。
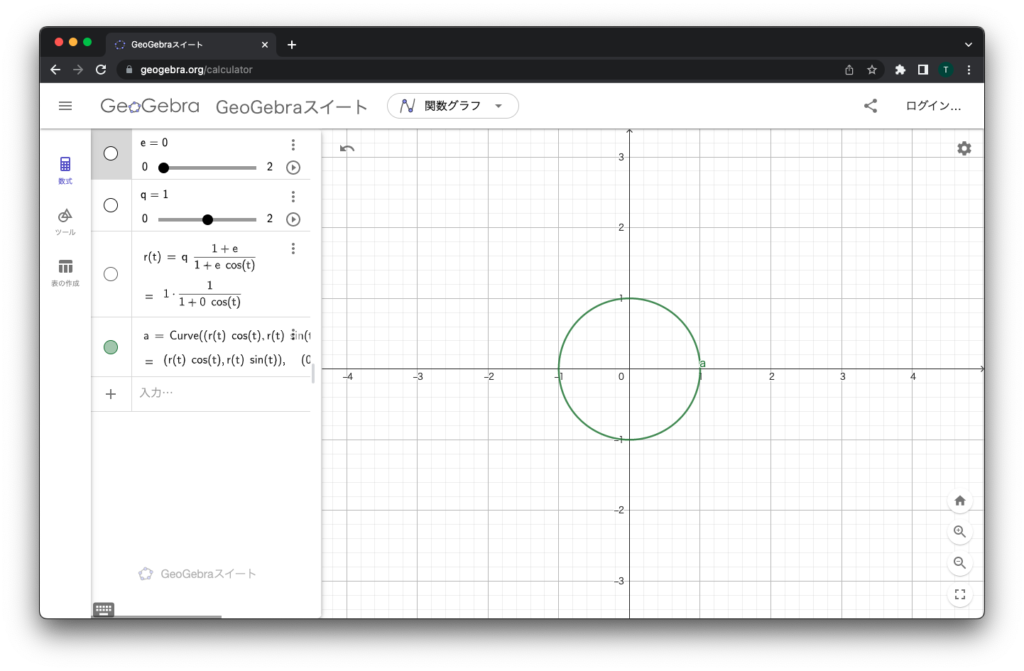
ちょっと小さいですが円になります。離心率 0 は円軌道です。
ここで近点距離 q を動かすと……円の大きさが変わります。近点距離は原点に一番近いときの距離ですが、そもそも円だと「一番近い」も何もないので、単純に半径が変わっているわけです。
数式に目を向けると、 e のところが 0 になった時には掛け算で色々 0 になって、結果以下のような数式に変わってしまうはずです。
$$r(t) = \frac{q ( 1 + 0 )}{1 + 0 \cos t} = q$$
今回の極座標の関数では、 t が角度で、r(t) は中心からの長さ(距離)を表現していたので、なるほど角度によらず距離が q になるのですね。確かにグラフに出る円の半径は q と一致しています。
近点距離を変えるとどうなる?
次は離心率を適当に…… 0.7 あたりにしてみましょう。また、近点距離も変えてみてください。
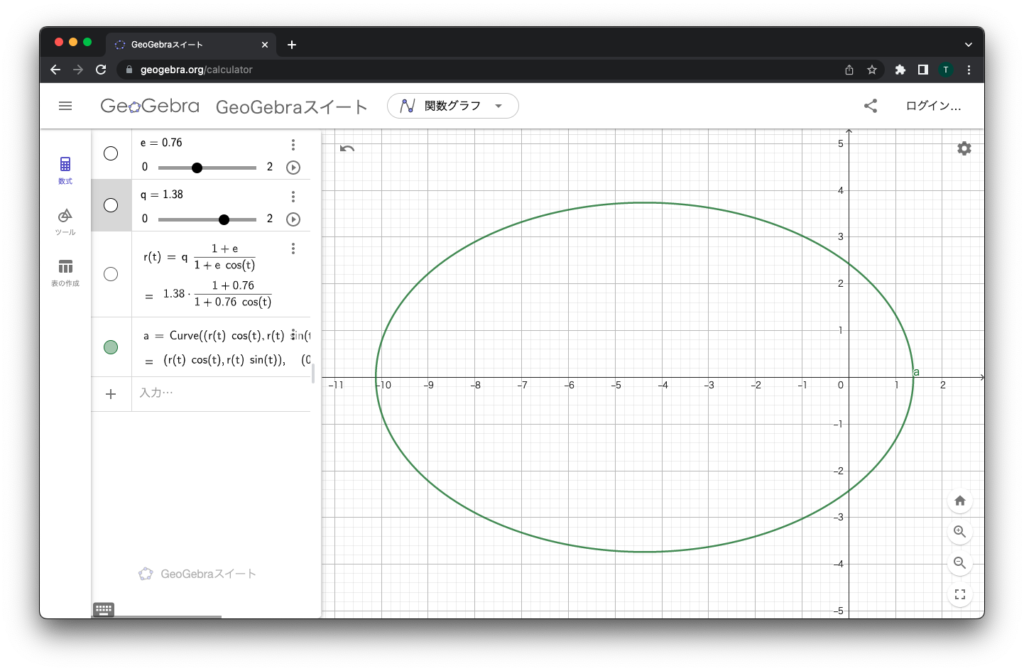
離心率が大きくなるにつれて、円が少しずつ潰れていきます。が、離心率を変えるだけだと、 x 軸との交点は変わりません。

ここが「近点」で、太陽の周りだったら「近日点」です。
近点距離を変えれば、この位置も変わりますね。離心率が楕円の形状を決めていることや、近点距離の意味を見て理解することができます。
どんどん変形させていって、離心率が1以上になると、軌道が丸まらずに広がってしまいます。
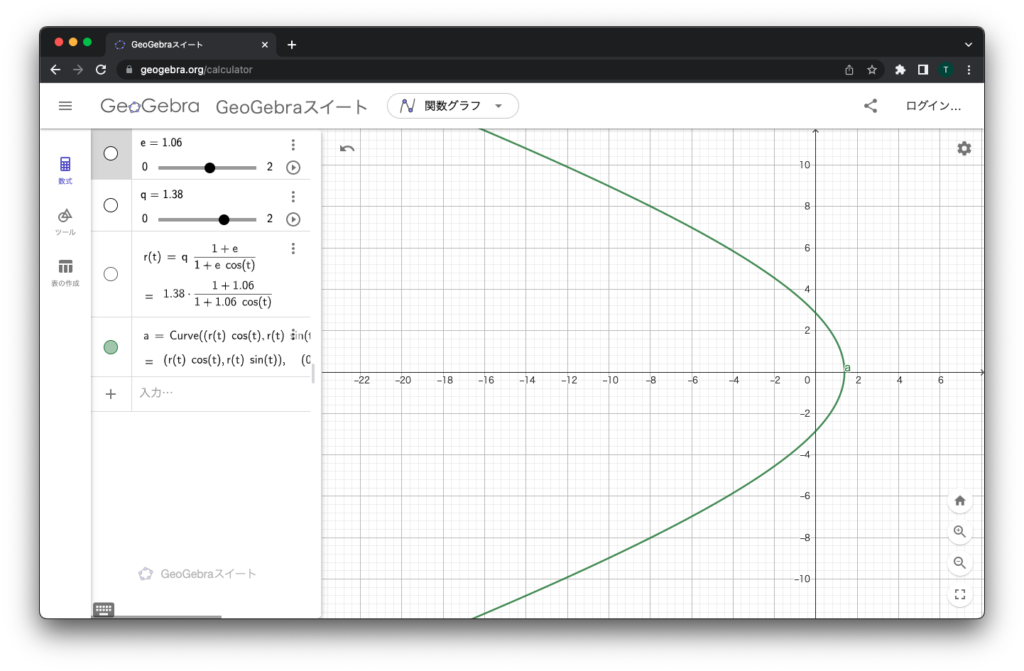
放物線軌道や双曲線軌道だと、一度太陽に近づいた後はもう戻ってこないということです。
また、近点距離を太陽に近づけていくと、カーブの曲がり方がキツくなります。
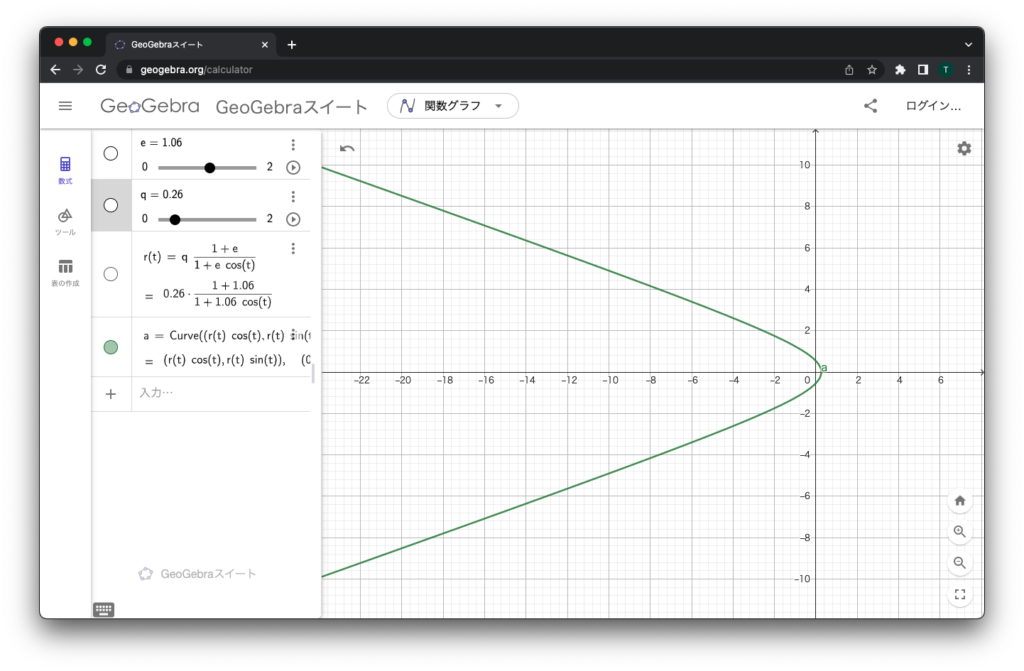
近づくほど強い重力の影響を受けて、進路が極端に変わるというわけです。

現実にはあまり近づきすぎると破壊されたり落ちたりして、それはそれで帰らぬ星になります。
なお、計算の都合上、逆側にも曲線が現れると思います。「双曲線」と呼ばれる所以ですが、現実の天体の軌道は左側のものだけです。
まとめ
今回は、軌道の形を表現している「二次曲線」を描かせて、パラメータを変化させながら様子を見ることで、パラメータの持つ意味などを確認しました。

数式の細かいところには触れていませんが、興味を持つきっかけになったでしょうか。
GeoGebraのような数式処理ソフトを使えば、プログラミングなどをしなくても、数式の様子を目で見て確認することができます。そして形を見ながら色々な部分を少し変化させてみると、数式の意味も少しわかってくるはずです。
謎の数式を見かけた時にも、コピペしてみたら何かわかるかもしれません。便利に活用してみてください!